Ühendav definitsioon
Liitmine on intressimäära arvutamise meetod, mis on tegelikult intressimäär, kui intress arvutatakse investeeringult / algsummalt, millele lisandub teenitud intress ja muud reinvesteeringud, teisisõnu, teenitud intress koguneb põhisummale, sõltuvalt hoiuse või laenu perioodist see võib toimuda kuu, kvartali või aasta kaupa
Proovime mõne põhinäite abil mõista, mis on liit ja kuidas see toimib
4 parimat näidet ühendamise võimest
Näide 1
Shane ja Mark otsustasid mõlemad investeerida 1 000 000 dollarit, kuid Shane otsustas investeerida lihtsasse intressi, Mark aga kümme aastat liitintressidesse 10% intressiga. Vaatame, mis juhtub kümne aasta pärast.
Lahendus:
Seega arvutatakse Shane'i investeering -

Teenitud summa kokku = 200 000 dollarit
Lihtsa intressiga saab Shane 10 aasta pärast 2 000 000 dollarit.
Markiinvesteering arvutatakse järgmiselt:

Teenitud summa kokku = 2,59,374 dollarit
Liitintressiga kasvab Marki investeeringuväärtus 2 599 374 dollarini.
Nüüd otsustas Shane investeerida selliste liitmeetodite abil nagu Mark, ja mõlemad investeerisid 2 000 000 dollarit 15% -lise määraga.
Shane'i investeeringu arvutamine on järgmine:

Teenitud summa kokku = 8,09,111,55 USD
Shane jääb investeerimiseks 10 aastaks ja saab lõpliku summa 8,09,111,55 dollarini 15% -lise määraga.
Markiinvesteering arvutatakse järgmiselt:

Teenitud summa kokku = 65,83,790,52 dollarit
Kuid Mark on kannatlikkusega pikaajaline investor ja jääb investeerima 25 aastaks ning tema investeeringuväärtus kasvab 65,83 790,52 dollarini
Ülaltoodud näide näitab liitmise jõudu. Mida pikem on investeerimisperiood, seda suurem on eksponentsiaalne kasv.
Näide 2 (iga nädal)
Simonil on 7500 dollarit kokkuhoidu ja poja kolledžifondi jaoks, kes kavatseb kolledžisse minna 15 aasta pärast, otsustas ta investeerida USA säästuvõlakirjadesse. Simoni eesmärk on säästa 20 000 dollarit ja USA hoiuvõlakirja aastane protsent on 6%. Mis on Simoni raha tulevane väärtus pärast 15 aastat?
Lahendus:
Arvestades
- Põhivõtja = 7500 dollarit
- Määr = 6% või 0,06
- Ajavahemik = 15 aastat.
- Mitu korda on see aastas suurenenud n = 52 nädalat
- Tuleviku väärtus =?
Seega arvutatakse tulevane väärtus -

Nädalase liitmise valem on järgmine.
F = P (1 + r / n) n * t- F = 7500 dollarit (1 + 0,06 / 52) 52 * 15
- F = 7500 dollarit (1 + 0,001153846) 780
- F = 18 437,45 dollarit
Nii et ülaltoodud arvutuste põhjal on selge, et Siimoni eesmärk säästa 20,00 dollarit ei saavutata ülaltoodud meetoditega, kuid see on sellele lähemal.
Pideva ühendamise meetod
Proovime nüüd ülaltoodud näidet pideva ühendi valemiga.
Seega arvutatakse tulevane väärtus -

- F = $ 7500e 0,06 * 15
- F = 7500e 0,9 dollarit
- Tuleviku väärtus (F) = 18 447,02 dollarit
Isegi pideva liitmise korral ei saavutata Simoni eesmärki säästa 20 000 dollarit poja kolledžifondi jaoks.
Vaatame igakuise liitvalemiga, et kui palju raha oli Simonil vaja investeerida, et saavutada eesmärk - säästa 20 000 dollarit 15 aasta jooksul 6% -lise krediidi kulukuse aastaga?
Seega arvutatakse tulevane väärtus -
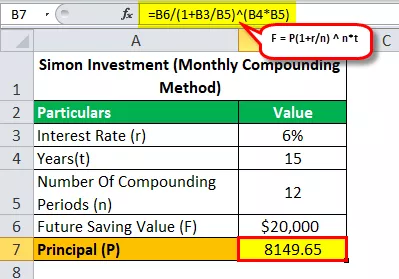
- 20 000 dollarit = P (1 + 0,06 / 12) 12 * 15
- P = 20 000 dollarit / (1 + 0,06 / 12) 12 * 15
- Põhivõtja (P) = 8149,65
Nii et ülaltoodud võrrandi lahendamisel saame vastuse, mis on 8 149,65 dollarit (summa, mille Simon peab investeerima, et saavutada oma eesmärk - säästa 20 000 dollarit 15 aastaga).
Näide 3 (tegelik aastakasum)
Oletame, et piiratud pank XYZ annab eakatele fikseeritud hoiuse eest 10% aastas ja eeldame, et pangaintressid lisanduvad kvartalite kaupa nagu kõik teised pangad. Arvutage efektiivne aastapõhine tootlus 5, 7 ja 10 aastaks.
Lahendus:
Aastane tootlus 5 aastat:
- t = 5 aastat
- n = 4 (kvartali liit)
- I = 10% aastas
Niisiis A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- I = 0,6386 viie aasta jooksul
Efektiivne intress = 0,6386 / 5
Efektiivne I = 12,772% aastas
Aastane tootlus 7 aastat:
- t = 7 aastat
- n = 4 (kvartali liit)
- I = 10% aastas
Niisiis A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1,9965
- I = 1,9965 seitsme aastaga
- Efektiivne I = 0,9965 / 7
Efektiivne I = 14,236% aastas
Aastane tootlus 10 aastat:
- t = 10 aastat
- n = 4 (kvartali liit)
- I = 10% aastas
Niisiis A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2,685
- I = 1,685 10 aastaga
- Efektiivne I = 1.685 / 10
Efektiivne I = 16,85% aastas
Näide 4 - (annuiteet: tulevane väärtus)
Iga kolme kuu tagant investeeritakse 1000 dollarit 4,8% aastas kvartalina. Kui palju on annuiteet 10 aasta pärast väärt?
Lahendus:
Nii et kui me ütleme, kui palju annuiteet 10 aasta pärast väärt on, tähendab see, et peame leidma tuleviku väärtuse ja see on oluline, sest alati, kui annuiteetide kohta on näide, peame nägema, mida peame välja selgitama.
Niisiis, Tuleviku väärtuse valem on
Annuiteedi FV = P ((1+ r) n - 1 / r)- P = Perioodiline makse
- r = määr perioodi kohta
- n = Perioodide arv
Nii et tulevikuväärtuse valem on
- Nii et siin P = 1000 dollarit
- r = 4,8% aastas või 0,048
- r (kord kvartalis) = 0,048 / 4
- r (kvartalis) = 0,012
- n = 10 aastat
- n (liitmise kordade arv) = 10 × 4 = 40
Seega arvutatakse annuiteedi FV -

Nii et nüüd FV = 1000 dollarit (1 + 0,012) 40-1 / 0,012)
Nii et ülaltoodud võrrandi lahendamisel saab FV 50 955,30 dollarit
Niisiis, kui palju on annuiteeti 10 aasta pärast ja vastus on 50 955,30 dollarit
Lisaks võime ka ülaltoodud näitest teada saada, kui palju intressi teenitakse 10 aasta jooksul.
Kuna investeeritakse 40 korda 1000 dollarit, siis on see koguinvesteering (40 × 1000 dollarit = 40 000 dollarit).
Seega intress = tulevikuväärtus - koguinvesteering
- Intress = 50 955,30 USD - 40 000 USD
- Intress = 10 955,30 dollarit
Nii et siin on oluline mõista, et annuiteetides saavad investorid palju huvi teenida. Ülaltoodud konkreetsetes näidetes annab 40 000 dollari suurune tagatisraha vastutasuks intressi 10 955,30 dollarit.
Märkus. Üksikasjalikuks arvutuseks saate alla laadida ülaltoodud Exceli malli.








