Milline on annuiteedi tulevane väärtus?
Tulevase annuiteedi tulevane väärtus on tulevikus laekuva summa väärtus, kus iga makse tehakse iga perioodi alguses ja selle arvutamise valemiks on iga annuiteetmakse summa korrutatud intressimääraga perioodide arvuks miinus üks, mis jagatakse intressimääraga ja tervik korrutatakse ühe pluss intressimääraga.
Annuiteedivormeli tulevane väärtus
Matemaatiliselt on see esindatud järgmiselt:
FVA Due = P * ((1 + r) n - 1) * (1 + r) / r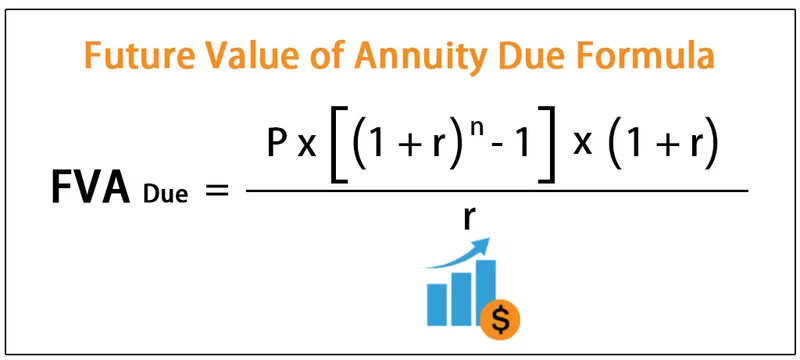
kus FVA Due = tasumisele kuuluva annuiteedi tulevane väärtus
- P = Perioodiline makse
- n = Perioodide arv
- r = tegelik intressimäär
Kuidas arvutada? (Samm sammu haaval)
- 1. samm: kõigepealt mõelge välja maksed, mis tuleb maksta igal perioodil. Pidage meeles, et ülaltoodud valem on kohaldatav ainult võrdsete perioodiliste maksete korral. Seda tähistab P.
- 2. samm: Järgmisena selgitage välja intressimäär, mis tuleb võtta levinud turumäära alusel. See on intressimäär, mille investor peab saama, kui raha investeeritakse turule. Efektiivse intressimäära saamiseks jagage aastapõhine intressimäär perioodiliste maksete arvuga aastas. Seda tähistatakse rie r = Aastane intressimäär / Perioodiliste maksete arv aastas
- 3. samm: Järgmisena arvutatakse perioodide koguarv korrutades perioodiliste maksete arv aastas ja aastate arv. Seda tähistatakse nie, n = aastate arv * Perioodiliste maksete arv aastas.
- 4. samm: lõpuks arvutatakse tasumisele kuuluva annuiteedi tulevane väärtus perioodilise makse (1. etapp), tegeliku intressimäära (2. etapp) ja perioodide arvu (3. etapp) põhjal, nagu eespool näidatud.
Näited
Näide 1
Võtame näiteks John Doe, kes kavatseb järgmise aasta seitsme aasta jooksul iga aasta alguses deponeerida 5000 dollarit, et säästa oma tütre hariduseks piisavalt raha. Määrake John Doe seitsme aasta lõpus kogunev summa. Pange tähele, et turu jätkuv intressimäär on 5%.
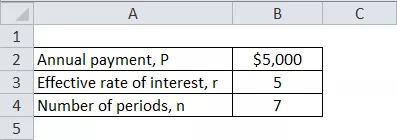
Arvutage perioodilise makse tasumisele kuuluva annuiteedi FV, kasutades ülaltoodud teavet,

FV of Pensionilepingute Due = P * ((1 + r) n - 1) * (1 + r) / r
= 5000 dollarit * ((1 + 5%) 7 - 1) * (1 + 5%) / 5%
Tähtajalise annuiteedi tulevane väärtus on -

= 42 745,54 dollarit ~ 42 746 dollarit
Seetõttu jääb John Doe seitsme aasta pärast oma tütre hariduseks kulutama 42 746 dollarit.
Näide 2
Võtame veel ühe näite Nixoni plaanidest koguda oma MBA jaoks piisavalt raha. Ta otsustab hoiustada järgmise nelja aasta jooksul (iga kuu alguseks) igakuise makse 2000 dollarit, et tal oleks võimalik koguda nõutav rahasumma. Haridusnõustaja kohta nõuab Nixon MBA jaoks 100 000 dollarit. Kontrollige, kas Nixoni hoiused rahastavad tema MBA-plaane, arvestades, et panga jätkuv intressimäär on 5%.

Arvestades
- Kuumakse, P = 2000 USD
- Efektiivne intressimäär, r = 5% / 12 = 0,42%
- Perioodide arv, n = 4 * 12 kuud = 48 kuud
Arvutage igakuise tasumisele kuuluva annuiteedi FV, kasutades ülaltoodud teavet,

= 2000 dollarit * ((1 + 0,42%) 48 - 1) * (1 + 0,42%) / 0,42%
Kuumakse tulevane väärtus on -
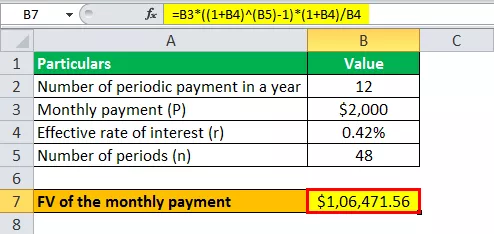
FV annuiteedi tõttu = $ 106,471.56 ~ $ 106.472
Planeeritud hoiuste korral on Nixonil eeldatavasti 106 472 dollarit, mis ületab tema MBA jaoks nõutavat summat (100 000 dollarit).
Asjakohasus ja kasutusalad
Võlgneva annuiteedi tulevane väärtus on TVM-i teine väljend. Täna saadud raha saab investeerida kohe, mis teatud aja jooksul kasvab. Üks selle silmatorkavamaid rakendusi on elukindlustuse kindlustusmaksete arvutamine. Samuti leiab see rakendust kindlustusfondi arvutamisel, kus igakuine palgamakse on perioodiline väljamakse. Annuiteetide tulevane väärtus kasvab kindlaksmääratud diskontomäära alusel. Seega, mida suurem on diskontomäär, seda suurem on annuiteedi tulevane väärtus.








