Mis on korrelatsioonikordaja?
Korrelatsioonikordajat kasutatakse selle määramiseks, kui tugev on suhe kahe muutuja vahel ja selle väärtused võivad olla vahemikus -1,0 kuni 1,0, kus -1,0 tähistab negatiivset korrelatsiooni ja +1,0 positiivset suhet. See võtab arvesse muutujate suhtelisi liikumisi ja määrab seejärel, kas nende vahel on mingeid seoseid.
Korrelatsioonikordaja valem
r = n (Σxy) - Σx Σy / √ (n * (Σx 2 - (Σx) 2 )) * (n * (Σy 2 - (Σy) 2 ))
Kus
- r = korrelatsioonikordaja
- n = vaatluste arv
- x = 1 silmus muutuva kontekstis
- y = teine muutuja
Selgitus
Kui kahe muutuja vahel on mingisugune seos või öeldakse seos, näitab see, kas üks muutujatest muutub väärtuseks, siis kipub ka teine muutuja väärtus muutuma, näiteks spetsiifiliselt, mis võib olla kas samas või vastupidises suunas. Võrrandi lugejaosa viib läbi koos liikuvate muutujate testi ja suhtelise tugevuse ning võrrandi nimetaja skaala skaalal, korrutades muutujate erinevused ruutu muutujatest.
Näited
Näide 1
Vaatleme kahte järgmist muutujat, x ja y, peate arvutama korrelatsioonikordaja.
Allpool on toodud andmed arvutamiseks.

Lahendus:
Kasutades ülaltoodud võrrandit, saame arvutada järgmise

Meil on kõik ülaltoodud tabeli väärtused n = 4.
Sisestame nüüd korrelatsioonikordaja arvutamise väärtused.

Seetõttu on arvutus järgmine,

r = (4 * 25 032,24) - (262,55 * 317,31) / √ ((4 * 20 855,74) - (262,55) 2 ) * ((4 * 30 058,55) - (317,31) 2 )
r = 16 820,21 / 16 831,57
Koefitsient on -

Koefitsient = 0,99932640
Näide 2
X riik on kasvava majandusega riik ja soovib läbi viia sõltumatu analüüsi oma keskpanga poolt intressimuutustega seotud otsuste kohta, kas need on inflatsiooni mõjutanud ja kas keskpank suudab seda kontrollida.
Järgnevalt on toodud intressimäära ja riigis keskmiselt valitsenud inflatsioonimäära kokkuvõte.
Allpool on toodud andmed arvutamiseks.

Riigipresident on pöördunud teie poole, et teha järgmisel kohtumisel analüüs ja esitada sama kohta ettekanne. Kasutage korrelatsiooni ja tehke kindlaks, kas keskpank on oma eesmärgi saavutanud või mitte.
Lahendus:
Eespool käsitletud valemi abil saame arvutada korrelatsioonikordaja. Intressimäära käsitlemine ühe muutujana, näiteks x, ja inflatsioonimäära käsitlemine teise muutujana kui y.

Meil on kõik ülaltoodud tabeli väärtused n = 6.
Sisestame nüüd korrelatsioonikordaja arvutamise väärtused.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Seos on -

Korrelatsioon = -0,92
Analüüs: Näib, et intressimäära ja inflatsioonimäära vaheline seos on negatiivne, mis näib olevat õige seos. Intressimäära tõustes inflatsioon väheneb, mis tähendab, et nad kipuvad liikuma üksteisest vastassuunas ning ülaltoodud tulemusest nähtub, et keskpank õnnestus intressipoliitikaga seotud otsust ellu viia.
Näide # 3
ABC labor uurib pikkust ja vanust ning soovis teada saada, kas nende vahel on mingeid seoseid. Nad on kogunud igasse kategooriasse 1000 inimese valimi ja mõelnud selle rühma keskmise pikkuse.
Allpool on toodud andmed korrelatsioonikordaja arvutamiseks.

Peate arvutama korrelatsioonikordaja ja jõudma järeldusele, et kui mõni seos on olemas.
Lahendus:
Vanuse käsitlemine ühe muutujana, näiteks x, ja kõrguse (cm-des) käsitlemine teise muutujana kui y.

Meil on kõik ülaltoodud tabeli väärtused n = 6.
Sisestame nüüd korrelatsioonikordaja arvutamise väärtused.

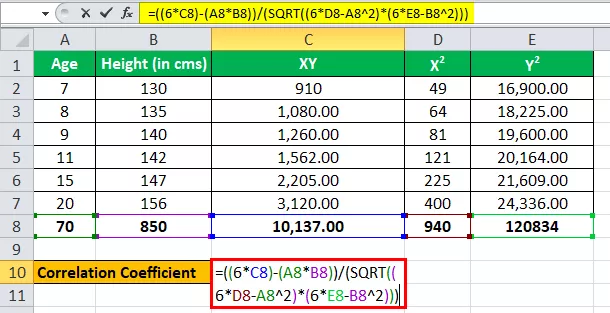
r = (6 * 10 137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20 834) - (850) 2 )
r = 1 322,00 / 1 361,23
Seos on -

Korrelatsioon = 0,971177099
Asjakohasus ja kasutamine
Seda kasutatakse statistikas peamiselt analüüsitavate muutujate vahelise seose tugevuse analüüsimiseks ning lisaks mõõdetakse ka seda, kas antud andmekogumite vahel on lineaarne seos ja kui hästi need võiksid olla omavahel seotud. Üks korrelatsioonis kasutatavatest tavalistest meetmetest on Pearsoni korrelatsioonikordaja.
Kui muutuja väärtus muutub koos selle muutuja väärtusega, siis on selle seose mõistmine kriitiline, kuna teise muutuja väärtuse muutuse ennustamiseks võib kasutada esimese muutuja väärtust. Korrelatsioonil on tänapäeva ajastul tänapäeval palju erinevaid kasutusviise, nagu seda kasutatakse finantstööstuses, teadusuuringutes ja kus mitte. Kuid on oluline teada, et korrelatsioonil on kolm peamist tüüpi suhteid. Esimene neist on positiivne seos, mis ütleb, et kui muutuja väärtuse muutus toimub, siis toimub muutus seotud muutujaga samas suunas. Samamoodi, kui on olemas negatiivne seos, käitub seotud muutuja vastupidises suunas. Samuti, kui korrelatsiooni pole, tähendab r ka nullväärtust.Mõiste paremaks mõistmiseks vaadake allolevaid pilte.









